MATLABで帯状の標準偏差をつけた折れ線グラフの作成方法についてご紹介します。
実際のコードも掲載しているのですぐに利用可能です。
標準偏差を持つデータ群の比較等にご利用ください。
なお、あくまで素人作成のコードですので利用は自己責任でお願いいたします。
帯状の標準偏差をつけた折れ線グラフ
コードの例
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | %% 帯状の標準偏差をつけた折れ線グラフ %データ生成 x(:,1)=0:10; for c=0:10 y1(c+1,:)=randi([1 10],1,5)+c; y2(c+1,:)=randi([1 10],1,5)+2*c; end Y1(:,1)=mean(y1(:,1:5),2); Y1(:,2)=std(y1(:,1:5),1,2); Y2(:,1)=mean(y2(:,1:5),2); Y2(:,2)=std(y2(:,1:5),1,2); %グラフ作成 figure(); fp = {'FontName', 'Arial', 'fontsize', 14','FontWeight','bold'} ; %平均値表示 plot(x,Y1(1:11,1),'Color','r','LineWidth',2.0); hold on plot(x,Y2(1:11,1),'Color','b','LineWidth',2.0); hold on %標準偏差表示 ar1=area(x,[Y1(1:11,1)-Y1(1:11,2) Y1(1:11,2)+Y1(1:11,2)]); hold on set(ar1(1),'FaceColor','None','LineStyle',':','EdgeColor','r') set(ar1(2),'FaceColor','r','FaceAlpha',0.2,'LineStyle',':','EdgeColor','r') ar2=area(x,[Y2(1:11,1)-Y2(1:11,2) Y2(1:11,2)+Y2(1:11,2)]); hold on set(ar2(1),'FaceColor','None','LineStyle',':','EdgeColor','b') set(ar2(2),'FaceColor','b','FaceAlpha',0.2,'LineStyle',':','EdgeColor','b') %軸などの設定 xlim([0 10]) ylim([0 30]) legend({'y1','y2'},'Location','northwest',fp{:},'fontsize', 12) xlabel('x', fp{:}, 'fontsize', 18) ylabel('y', fp{:}, 'fontsize', 18) ax = gca; ax.XAxis(1).Color = [0 0 0]; set(gca,'FontWeight','bold'); set(gca,'FontSize',14); set(gca,'linewidth',1.5); title('帯状折れ線グラフ',fp{:},'fontsize', 20) %画像として保存 cd figure saveas(gcf,'std','png') cd .. |
ざっくりとコードで行っている作業の手順は次の通りです。
- 乱数を使用してデータを生成（y1,y2）
- 平均値と標準偏差を算出
- データの平均値をグラフ化
- 標準偏差の帯をグラフに追加
- 軸の設定
- 画像として保存
帯状の標準偏差を持つ折れ線グラフに重要なのが④です。
この部分で何を行なっているかざっくり説明していきます。
1 2 3 4 | %標準偏差表示 ar1=area(x,[Y1(1:11,1)-Y1(1:11,2) Y1(1:11,2)+Y1(1:11,2)]); hold on set(ar1(1),'FaceColor','None','LineStyle',':','EdgeColor','r') set(ar1(2),'FaceColor','r','FaceAlpha',0.2,'LineStyle',':','EdgeColor','r') |
「area」を使って指定した範囲を塗りつぶします。
ここでは[(平均値-標準偏差)から(平均値+標準偏差)を塗りつぶす]と指示しています。
なお、areaでの表記は[(平均値-標準偏差)から上に(標準偏差×2)の幅の帯を描画]とします。
「set(ar(1)…」では帯の下側の範囲、つまり(平均値-標準偏差)以下の範囲のパラメータを指定します。
そのため、塗りつぶしなし、縁のみパラメータを指定しています。
一方で「set(ar(2)…」では帯の内部のパラメータを指定するため、’FaceColor’を指定します。
ここで、’FaceAlpha’で帯の透過度を指定し、’LineStyle’で帯の縁の線を指定しています
出力結果
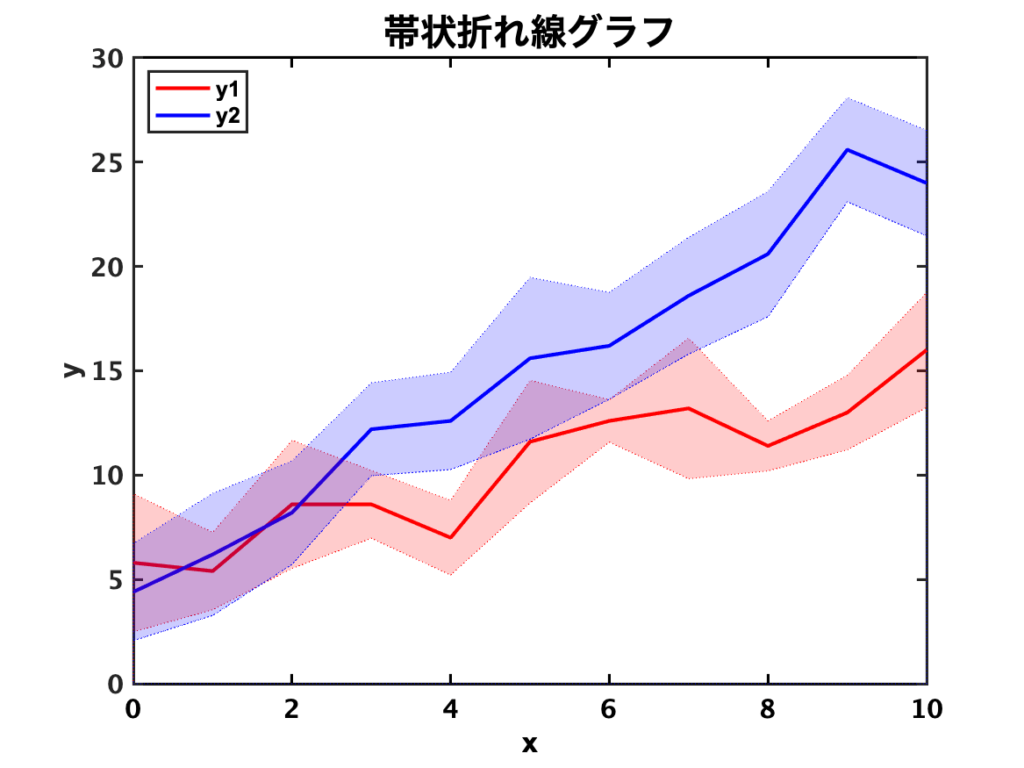
上の図が、上記コードの実行結果です。
乱数で作成したy1,y2のデータに対して、平均値と標準偏差の帯を表示することができています。
今回はrand関数を使用してデータをグラフ作成を行いました。
実際に使用する際には、y1,y2の部分に自分のデータを当てはめてみてください。
なお、使用する際は自己責任でお願いします。
さいごに
以上がMATLABで95%等確率楕円/信頼楕円の作成方法です。
自分なりに試行錯誤して作成したコードですが、間違いを含んでいる可能性があります。
間違いの指摘やコメントがありましたら本記事のコメント欄にお願いします。
最後までお読みいただきありがとうございました。